- September 23, 2018
- brightsandz
- Cell tower radiation
We, at Brightsandz do mobile phone tower RF radiation audits. We meet a lot of people who are concerned about mobile phone towers around their homes and work spaces. In this blog, We try answering the question – what is a safe distance from a mobile phone tower.
Spoiler: For a quick answer in metres distance scroll below and read the conclusion.
Introduction
Living near cell phone tower is not healthy. There are multiple health risks associated with living near cell phone tower. Cell phone towers communicate by use of pulsed microwave signals with each other. WHO (World health organization) and IARC (International agency for research on Cancer) declared radio frequency radiation (RFR) to be cancer causing in May 2011. Even while RFR is associated with same level of carcinogenicity as Lead, Sulphur fumes and Vehicle Exhaust, there are many who question this (cancer) premise. So the debate ranges. In the mean time, we advocate use of the precautionary principle. Better safe than worry.
Safe distance from a mobile phone tower – Making sense of the antennas
Not all mobile antennas are the same. There is a difference between a receiving antenna and a transmitting antenna. The most usual way to make out is the difference in space. A receiving antenna is generally circular or elliptical in space. Whereas, a transmitting antenna is cuboid, squarish or rectangular in shape.

Not all mobile antennas radiate the same frequency. One antenna could be radiating at 800 MHz whereas another could be radiating at 2300MHz or 2.3GHz. As a thumb rule the higher the radiating frequency, the higher will be the radiated energy. Therefore, in terms of radiation – a 800MHz antenna radiates lesser energy as compared to 2.3Ghz antenna.
Natural and artificial barriers to mobile phone tower radiation
RF radiation intensity falls with concrete or even natural barriers (stone, rock, dense foliage). Therefore if the tower is not in direct line of sight, there are chances that the radiation will be low.
In some cases for better connectivity – antennas are tilted around vertical axis. Such a tilt can change the plane of radiation and therefore concentrate high RF radiation in the direction of the tilt.
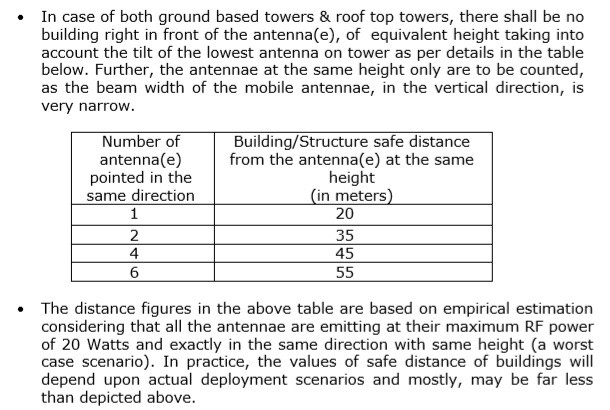
Number of antennas pointing at the building or living area
RF Radiation directed at you also depends upon the number of antennas that are facing towards you. Generally a higher number of antennas facing you will mean higher degree of radiation incident on you. In India, the department of telecom (DoT) has a distance advisory for number of antenna in the same direction from any building or human housing structure.
Shadow zones near mobile phone towers
A mobile phone antenna has a radiating pattern. It transmits higher energy in the blue shaded lobes. This emission intensity falls with distance. It also falls if you are not directly in any of the radiation lobes. The shadow zone is an area which falls out of the radiation lobe of an antenna. Alternatively, the highest radiation exposure is at the primary lobe at about 50 metres from the radiating antenna.
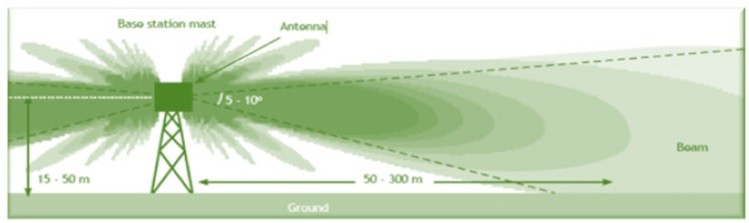
Any area not in the primary lobe falls in the shadow zone – which does not receive high radiation
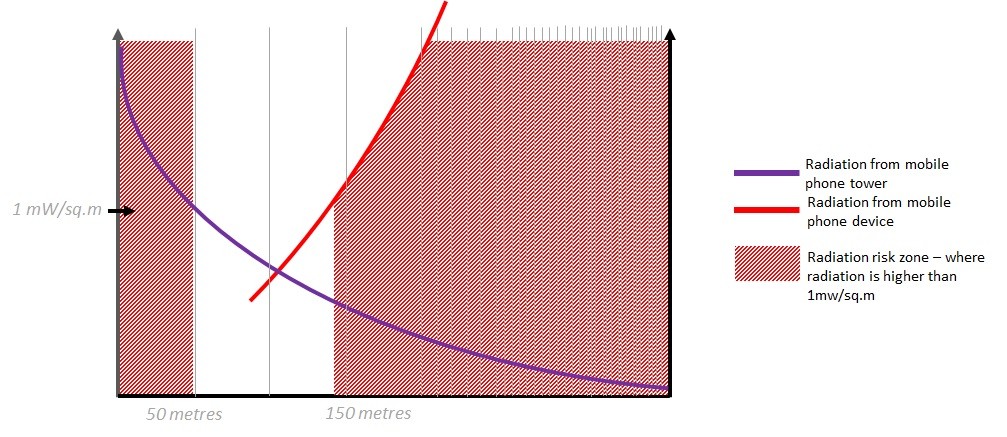
Radiation from mobile phone tower (Purple Line) reduces exponentially with distance. Within 50 metres, it is higher than the exposure limiting value. This area around a cell phone tower could be dangerous in terms of high radiation from the tower.
However, as we start going further away from the tower, and the tower signal (Purple line) drops, the Phone radiation levels (Red line) start increasing. At around the 150 metre mark, phone radiation levels go beyond the exposure limiting value. For the rest of the distance – phone radiation remains pretty high. This is more damaging because it is closer to the brain side.
What is the safe distance from a mobile phone tower?
Radiation power is typically the strongest at 50 metres distance from the antenna and it keeps falling. After 150 metre, it becomes weak (Refer to diagram below). Post that the cell phone has to do more work to reach out to the radiated signals. Therefore in shadow zones (refer to point) and at longer distances from cell towers, instances of call drops increase.
Perhaps the most critical point here is that when radiation power from mobile tower antennas fall, there is a consequent increase in radiation levels from mobile phones and cell phones. A mobile phone antenna radiates at 80-160 Watt/ sq.m. However it has a high distance of separation. Whereas, a mobile phone radiates at <1 Watt/ sq.m. However it is only a few millimeters away from the head space/ brain cavity. In such a condition, when the phone is radiating at a high, the absorption of radiation by the brain is multiple times higher than that of radiation absorbed from mobile phone tower emission.
To summarize, radiation from a mobile phone tower, is 24*365 slow roast. This can be mitigated by avoiding line of sight or shielding procedures. We have known of instances in Mumbai, Okhla, GKII, Maharani Bagh (New Delhi) where high proximity to cell tower have led to cases of cancer.
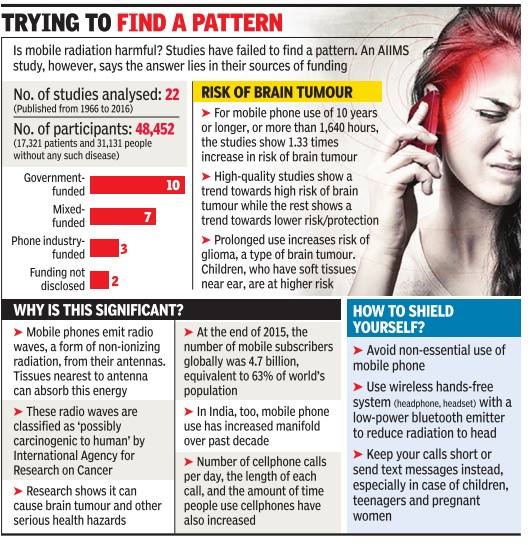
However, the greater risk is the damage from our own mobile phones in places where the mobile network coverage is not strong enough. This has a greater bearing on individual health raising concerns of cluster headaches, deafness, tinnitus and even Brain tumor. All India Institute of Medical Sciences, New Delhi has set a limit of less than 45 minutes talk time on the mobile phone when it is placed close to the ear beside the head. The study states a 33% increase in brain tumor rates for heavy cellphone users.
In conclusion
The safe distance from a mobile phone tower is not an objective answer. There are multiple factors that affect mobile radiation intensity. As a thumb rule, anyone in 150 metre radius could be under risk. And if the tower is 300 metres or more distant, this could lead to weak coverage – leading to signal drops. Ironically most of the times, we are more concerned by the mobile phone tower 300 metres away from us and choose to be blissfully ignorant about the mini cell tower that we carry on ourselves through the day – the cellphones.
Categories
- 5G (2)
- Anti Radiation Mobile Phone Chips (1)
- Cell tower radiation (6)
- Data centre radiation (1)
- Devices and EMF Radiation (13)
- Ecology hazards of EMF Radiation (5)
- EMF and new technologies (2)
- EMF Radiation and Autism (2)
- EMF Radiation and Pregnancy (3)
- Health hazards of EMF radiation (15)
- Laptop Radiation Shield (2)
- Magnetic frequency (2)
- Radiation Premise Audit (2)
- RFID isolation (1)
- Uncategorized (5)